2次元平面および3次元空間における直線の方程式を紹介します.平面の方程式を紹介します.2次元平面および3次元空間における点と直線の距離を計算するための数式を紹介します.点から直線に降ろしたときの垂線との交点の座標を計算する数式も紹介します.点と平面の距離も紹介します.点から平面に降ろした垂線との交点も紹介します.2次元平面および3次元空間における直線と直線の交点の数式を紹介します.
点![]() を通り,単位ベクトル
を通り,単位ベクトル![]() に平行な直線上の点
に平行な直線上の点![]() は,媒介変数
は,媒介変数![]() を使って,以下のように表現される.
を使って,以下のように表現される.
![]()
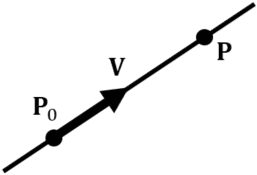
点![]() とし,単位ベクトル
とし,単位ベクトル![]() とし,点
とし,点![]() として式変形すると以下のように表現される.
として式変形すると以下のように表現される.
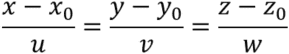
2次元の場合は![]() すなわち
すなわち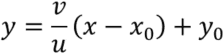 となる.
となる.
点![]() と点
と点![]() を通る直線上の点
を通る直線上の点![]() は,媒介変数
は,媒介変数![]() を使って,以下のように表現される.
を使って,以下のように表現される.
![]()

点![]() および点
および点![]() として式変形すると以下のように表現される.
として式変形すると以下のように表現される.
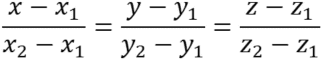
2次元の場合は![]() すなわち
すなわち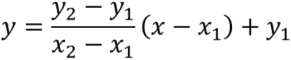 となる.
となる.
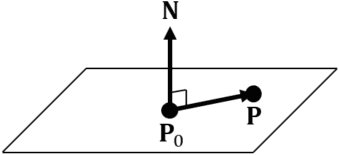
単位法線ベクトルが![]() であり,点
であり,点![]() を含む平面上の点
を含む平面上の点![]() は以下のように表現できる.
は以下のように表現できる.
![]()
点![]() とし,単位ベクトル
とし,単位ベクトル![]() とし,点
とし,点![]() として式変形すると以下のように表現される.
として式変形すると以下のように表現される.
![]()
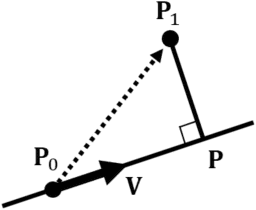
点![]() から直線に垂線を降ろしたときの交点
から直線に垂線を降ろしたときの交点![]() の座標は以下のように計算できる.なお,当然
の座標は以下のように計算できる.なお,当然![]() は単位ベクトルでなければいけない.
は単位ベクトルでなければいけない.
![]()
よって,点と直線の距離は上記の![]() を用いて以下のように計算できる.
を用いて以下のように計算できる.
![]()
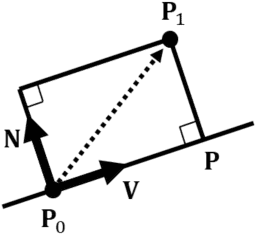
点![]() を通り,単位ベクトル
を通り,単位ベクトル![]() に平行な直線を考える.ベクトル
に平行な直線を考える.ベクトル![]() に直交する単位ベクトル
に直交する単位ベクトル![]() を定義すると,点と直線の距離は以下のように表される.
を定義すると,点と直線の距離は以下のように表される.
![]()
![]()
ところで直線の方程式は![]() すなわち
すなわち![]() であった.
であった.
ここで,![]() ,
,![]() ,
,![]() のように再定義すると直線の方程式は以下のように表現できる.
のように再定義すると直線の方程式は以下のように表現できる.
![]()
点と直線の距離![]() を
を![]() ,
,![]() ,
,![]() で表すと以下のようになる.
で表すと以下のようになる.
![]()
つまり,点![]() と直線
と直線![]() の距離は,
の距離は,![]() が成り立っているとき
が成り立っているとき
![]()
である.
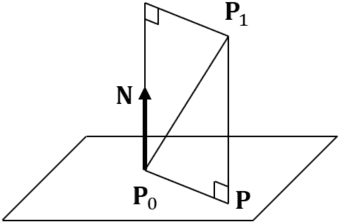
点![]() から平面に垂線を降ろしたときの交点
から平面に垂線を降ろしたときの交点![]() の座標は以下のように計算できる.なお,当然
の座標は以下のように計算できる.なお,当然![]() は単位ベクトルでなければいけない.
は単位ベクトルでなければいけない.
![]()
また,点と平面の距離は以下のように計算できる.
![]()
![]()
ところで,平面の方程式は![]() すなわち
すなわち![]() であった.
であった.
ここで,![]() ,
,![]() ,
,![]() ,
,![]() のように再定義すると平面の方程式は以下のように表現できる.
のように再定義すると平面の方程式は以下のように表現できる.
![]()
つまり,点![]() と平面
と平面![]() の距離は,
の距離は,![]() が成り立っているとき
が成り立っているとき
![]()
である.
直線![]() と直線
と直線![]() の交点は以下の通り.
の交点は以下の通り.
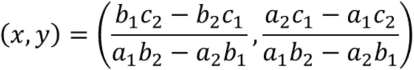
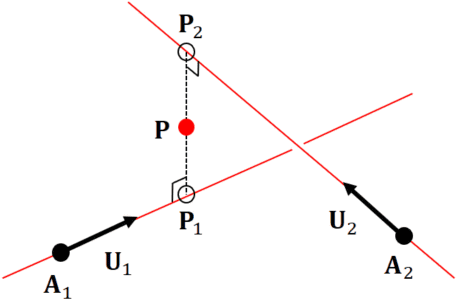
3次元の直線![]() と直線
と直線![]() の交点
の交点![]() を求める.
を求める.![]() と
と![]() は単位ベクトルである.3次元の2直線は一般に交点を持たない.2直線と最も近い点を求める.
は単位ベクトルである.3次元の2直線は一般に交点を持たない.2直線と最も近い点を求める.
点![]() は
は![]() に最も近くなければいけないので
に最も近くなければいけないので![]() .点
.点![]() は
は![]() に最も近くなければいけないので
に最も近くなければいけないので![]() .よって,以下が導出される.
.よって,以下が導出される.
![]()
すなわち
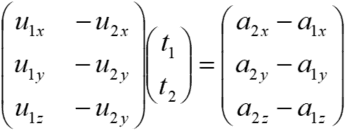
または
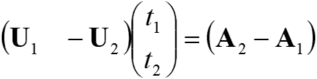
両辺に左から![]() をかけると
をかけると

よって以下が成り立つ.
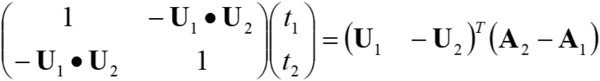
これを解くと以下のようになる.
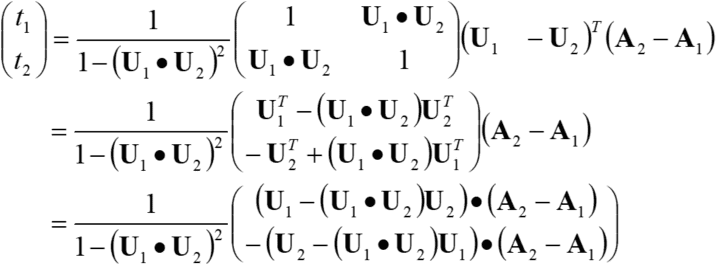
![]() と
と![]() の両方をできる限り満たす解は
の両方をできる限り満たす解は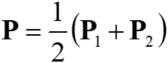 である.この式に上記の式を代入すると交点の座標が以下のように表される.
である.この式に上記の式を代入すると交点の座標が以下のように表される.
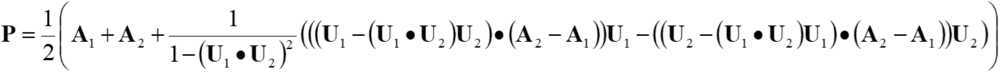
ここで,![]() だが,
だが,
![]() のときは交点が求まり,
のときは交点が求まり,
![]() のときは2つの直線は平行なので交点が存在しない.
のときは2つの直線は平行なので交点が存在しない.