Rotation matrix representation

Tweet

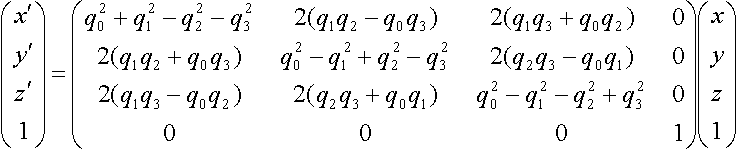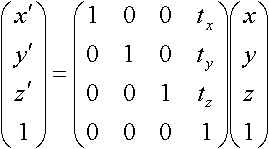
Transformation matrices of 3D objects are shown here. Especially, the rotation matrix in 3D space is shown. Rotation matrix is represented by 3-by-3 matrix, and often represented by Euler angle, quaternion, or Rodrigues' formula. Matrices which rotate 3D shapes about the x-, y-, or z-axis are also shown.

Translation

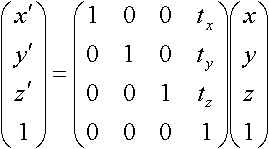
Scaling, Reverse

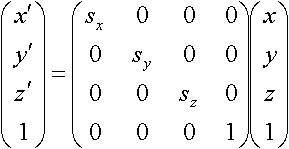
Rotate alpha around x axis

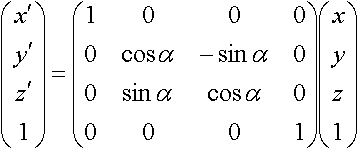
Rotate beta around y axis

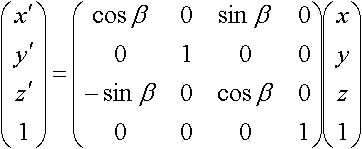
Rotate gamma around z axis

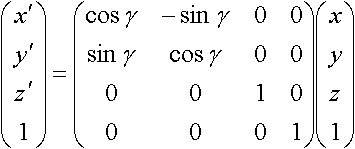
Rotate by Euler angle: alpha, beta, gamma

Depends on rotation axes

Rotate by Roll (phi), Pitch (theta), Yaw (psi)

Depends on rotation axes

Rotate by: vector direction = rotation axis, vector length = rotation angle (Rodrigues' formula)

Unnormalized vector v=(v_x,v_y,v_z), rotation angle theta=|v|.

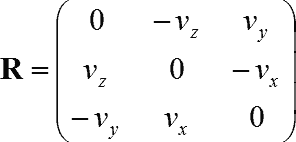
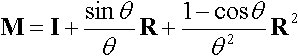
For the case when theta is nearly zero.

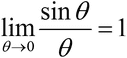
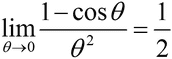
Rotate theta around the unit vector (v_x,v_y,v_z) (Rodrigues' formula)

Unit vector v=(v_x,v_y,v_z), rotation angle theta.

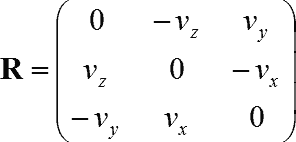
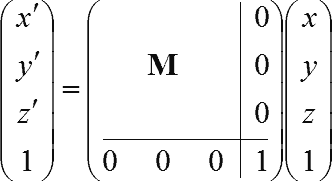
Rotate theta around the unit vector (n_x,n_y,n_z)

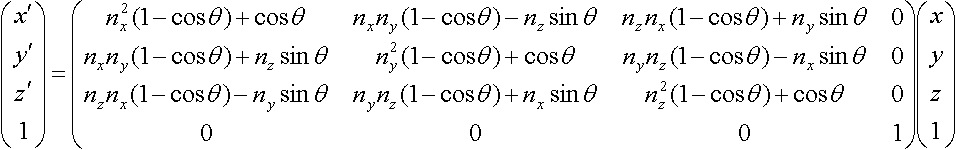
Rotate by quaternion

Quaternion q=(q₀,q₁,q₂,q₃), where |q|=1.

Back