Here, I introduce a method to fit a plane to 3D point cloud.
Denote P as a point on a plane. The unit normal vector of a plane is N. A certain point P0 is on the plane. Then, the 3D plane is expressed as follows.
![]()
First, calculate the barycenter of the point cloud, and let it as P0. Namely, P0 is calculated as follows using the point cloud P1, P2, ..., PM.
![]()
Here, I denote the 3D coordinates of P0 as (x0,y0,z0). Denote the 3D coordinates of point cloud as P1=(x1,y1,z1), P2=(x2, y2, z2), ..., PM=(xM, yM, zM). What we want to solve is N=(Nx, Ny, Nz) which satisfies the following.
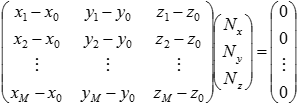
This is represented as follows.
![]()
The rank of M*3 matrix A is 2. Apply SVD (singular value decomposition) to A, and we have the solution to N, which is the right singular vector whose singular value is the smallest.